과학을 잘 모르지만 과학을 좋아하고, 수포자이지만 수학을 좋아하는 제가 최근에 저를 사로잡은 내용이 있었습니다.
이름하여 바로 ‘리만 가설’ 입니다.
리만 가설 (Riemann hypothesis)
개발자 블로그에 무슨 뚱딴지 같은 이야기라구요? 수학을 잘 모르지만 개발자가 된 이상 간단한 4칙연산 뿐만 아니라
점점 더 어려운 고등수학을 살짝 발 담을 일이 많아집니다. (잘 모르셨겠지만요)
일단 리만 가설이라는 것을 알아봅시다.
리만 제타 추측은 리만 제타 함수의 모든 자명하지 않은 영점의 실수부가 1/2 이라는 추측이다.
아니 이게 무슨 말일까요…

소수 (prime number)
먼저 ‘소수’ 라는 개념을 알아야 합니다.
소수의 정의는 다음과 같습니다.
1과 자기 자신으로밖에 나누어 떨어지지 않고 자기 자신의 곱셈의 역수가 없는 수
간단히 말해서 2, 3, 5, 7, 9 (369 아닙니다), 11 … 등과 같이 나눠지지 않는 수를 의미합니다.
아주 작은 소수는 찾기가 쉽지만, 큰 소수를 찾을려면 소인수 분해를 해야 합니다.
소인수 분해 (integer factorization)
다들 중학교 수학이 기억이 안날 수 있어서, 복습하는 차원에서 적어봅니다.
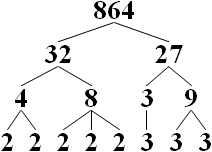
소인수 분해란 1 보다 큰 자연수를 소인수(소수인 인수)들만의 곱으로 나타내는 것으로
가장 쉬운 방법은 작은 소수 부터 (2, 3, …) 으로 부터 하나씩 나눠봐야 합니다.
문제는 현대의 컴퓨터상에서 이 소인수분해를 빠르게 할 알고리즘이 없는 것 입니다.
그래서 이런 난해한걸 어디에서 쓰나요?
위의 문단의 내용처럼 현대 컴퓨터에서는 소인수 분해를 빠르게 할 알고리즘이 없습니다.
예를 들어 193자리 수는 5개월간 30개의 2.2 GHz 옵테론 CPU를 동원하여 소인수분해가 되었습니다.
소인수분해의 난해함은 RSA와 같은 현대 암호의 핵심적 부분이 됩니다.
저희가 쓰는 이렇게 쓰는 인터넷도 전자상거래도 이 소수 기반의 보안 으로 이루어 진 것이죠.
소수의 규칙을 찾기 위한 노력, 오일러의 공식
고대부터 이 소수의 매력에 많은 수학자들이 접근하여 소수의 규칙성을 찾기 시작했습니다.
그렇지만 아무리 접근해봐도 소수는 예측할 수 없다고 생각될 뿐이었습니다.
그런 와중에 오일러라는 분이 소수를 가지고 곱했다 뺐다 했더니 원주율이 나오네? 라는 접근을 하게 되었습니다.
하지만 ‘오일러의 공식’으로 유명한 수학자 레온하르트 오일러(1707~1783)는 소수를 관찰하면서 소수로만 이뤄진 식을 하나 만들었다. 소수의 제곱을 소수의 제곱에서 1을 뺀 수로 나눈 뒤 끊임없이 곱하는 식(1번 식)을 정리했더니 ‘파이(원주율)’가 나타났다.
바로 이것이 ‘오일러의 공식’ 으로 불리우는 유명한 발견 이었습니다.
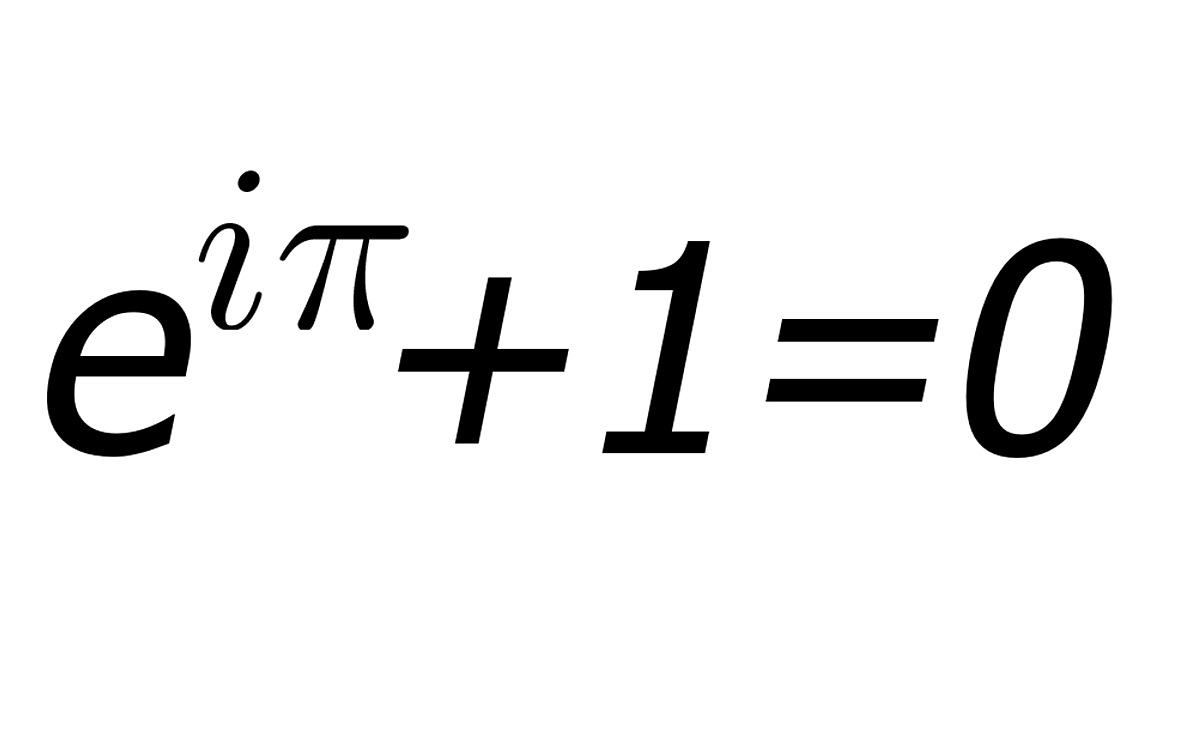
가우스의 소수 정리

천재 수학자였던 가우스는 벌써부터 남다른 능력으로 하루에 천개씩 직접 손으로 찾아가며 소수의 빈도수를 계산해냅니다.
당시 그의 나이 15살…
리만, 스승 가우스의 소수 정리를 마무리하다
드디어 리만 가설의 주인공인 리만이 여기서 등장을 하게 됩니다.
리만은 오일러의 함수를 변형하여 입체적인 그래프를 만드는데, 놀랍게도 이 그래프에서 리만이 계산한 4개의 비자명 근이 복소평면 위에서 모두 일직선상에 있었습니다. 무슨 말이야
그래서 소수의 비밀을 알면 어떻게 되는데?
여튼 저는 수학을 잘 모르기 때문에, 약 400년간 많은 수학자들이 리만 가설을 도전하였고,
또한 고대부터 소수의 비밀을 풀기 위해서 노력했습니다.
사실 소수의 비밀을 못 알아낼지도 모릅니다.
다만 위의 오일러의 공식에서 돌출한 원주율 뿐만 아니라, 최근에는 양자물리학에서 쓰이던 공식이 리만 가설의 공식과 동일하다는 내용이 알려지면서… 단순히 수학자들의 놀이 일뿐이 아니라 자연의 숨겨진 비밀을 푸는 열쇠가 될지도 모른다는 생각을 하게 되었습니다.

혹시 ai 가 소수의 패턴을 알 수 있지 않을까?
그렇다면 혹시 패턴이 있다면 ai 가 소수의 패턴을 알 수 있지 않을까 라는 생각으로 접근하게 되었습니다.
하지만 결론은 No 입니다.
왜냐고요?
머신러닝은 모든 것에 대한 해결책이 될 수 없으며. 머신러닝 자체는 데이터에서 부터 배우는 것인데 문제는 우리가 머신러닝을 학습시킬려면 우리가 학습하도록 가르칠 수 있는 데이터 패턴이 필요하다는 것입니다.
앞서 말해서, 소수의 정의를 알아봤고, 그 소수의 패턴을 알 수가 없는것을 알아왔습니다.
오히려 패턴을 알기 위해, 데이터의 패턴을 알려줘야 하는 모순에 봉착한 것이죠.
그냥 무시하고 머신러닝 알고리즘을 훈련 시키려고 해도 입력한 데이터에 가까운 무언가만 가지게 될 것이며. 실제 예측이랑 터무니 없는 답만 나올 것이기 때문입니다.
따라서 우리가 정확한 소수를 찾을려면 이미 계산할 정확한 방법이 있을 때 쓸 수 있는거지,
우리가 알지도 못하는 것을 제시하는건 안되는 것이었습니다…

Ref.