몬티홀 문제
넷플릭스의 드라마 D.P.에 ‘몬티홀 문제’ 라는 에피소드가 있습니다.
에피소드를 보면 몬티홀 문제에 대한 언급이 나오는데 도저히 이해가 안되서 인터넷에 찾아보기 시작했습니다.
몬티홀 문제란? 나무위키 에 정리된 내용에 따르면
- 문 3개가 있는데 한 문 뒤에는 자동차가 있고 나머지 두 문 뒤에는 염소가 있다.
- 참가자는 이 상황에서 문을 하나 선택하여 그 뒤에 있는 상품을 얻는다.
- 참가자가 어떤 문을 선택하면 사회자는 나머지 두 문 중에 염소가 있는 문 한 개를 열어 참가자에게 그 문에 염소가 있다고 확인시켜준다.
- 그 후 사회자는 참가자에게 선택한 문을 닫혀있는 다른 문으로 선택을 바꿀 기회를 준다.
이때 선택을 바꾸는 쪽이 이득일까요?, 유지하는 쪽이 이득일까요?
정답은 바꾸는 쪽이 2/3 확률로 유리합니다.
일반적으로 생각했을때 남은 문 하나에는 염소, 나머지 하나는 자동차니까 1/2 확률이라고 생각하기 쉽습니다.
아래의 그림을 참조해서 설명을 하면
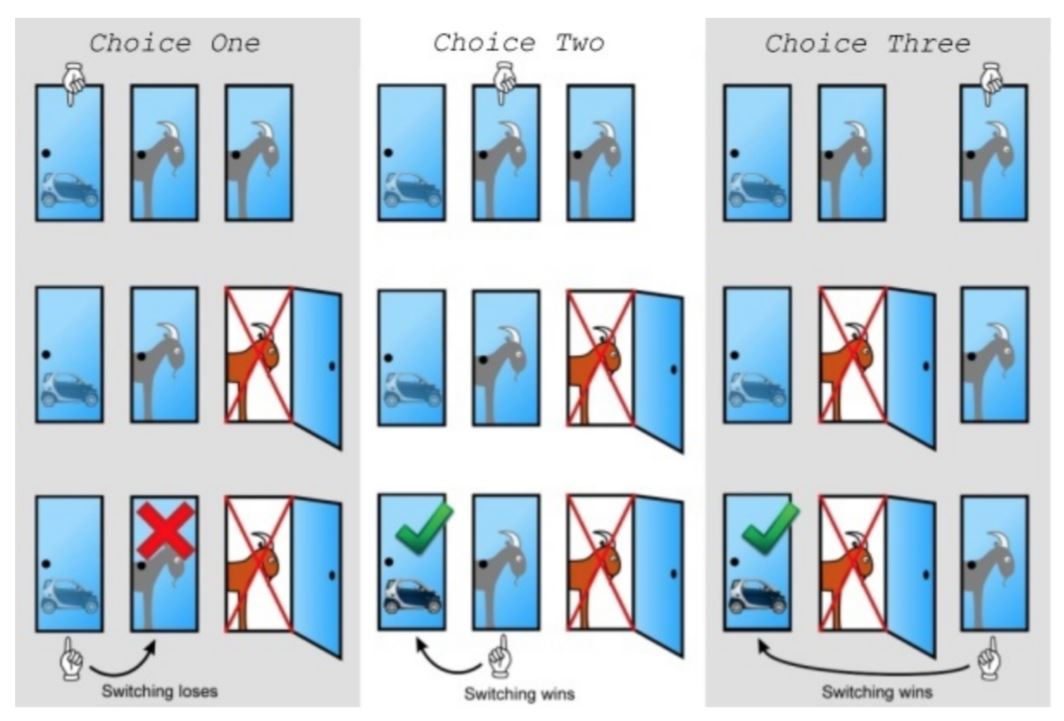
- 첫번째 선택일 경우 바꿀 경우 염소를 선택하게 됩니다.
- 두번째 선택일 경우 바꿀 경우 자동차를 선택하게 됩니다.
- 세번째 선택일 경우 바꿀 경우 자동차를 선택하게 됩니다.
그래서 바꾸는 쪽이 확률이 2/3로 유리합니다.
이렇게 보니 조금은 이해가 됩니다.

관련해서 이것저것 검색하다보니 해당문제가 통계학의 영역이란걸 알게 되었고,
빅데이터가 대두되면서 동시에 중요도가 높아지고 있습니다.
통계학 > 빅데이터 > 파이썬 개발자에게 도움이 되겠다는 식의 빌드를 타게 되어 이번 포스트를 작성하게 되었습니다.

확률과 통계
‘확률과 통계’ 라고 하면 고등학교 수학과정 어디인가에 있었던 걸로 기억되시는 분들이 많으실겁니다.
순열, 이항정리, 확률분포등등 있었던것 같은데, 우리는 수능을 다시 볼게 아니니 일단 넘어가도록 합니다.
회사의 연봉에 대해서 각 부서별로 통계를 내본다고 한다면
- 사원들의 연봉 데이터를 모으고
- 연봉 데이터를 부서별로 정리해서
- 도표나 그래프등으로 시각화
하는 과정을 거치게 됩니다.
이렇게 전체데이터를 모아서 그 특징을 기술 하는 것을 기술통계학이라고 합니다.
하지만 이렇게 통계를 내었을때
영업1팀 A는 1000, B는 70, C는 80…
영업2팀 A는 150, B는 270, C는 140…
라는 통계만으로는 한 눈에 파악되지 않습니다.
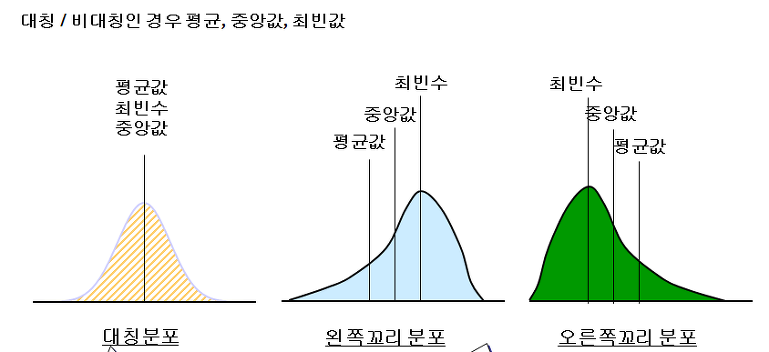
이럴때 한눈에 파악하기 위해 사용 하는 것이 평균, 중앙 값 최빈 값이 있습니다.
- 평균 값 : 전체 수를 더하고 이를 데이터의 수로 나눈 값
- 중앙 값 : 데이터를 나열 했을 떄 한가운데 있는 값
- 최빈 값 : 데이터 중에서 가장 빈도가 높은 값
평균 값으로 내었을때 영업 1팀의 평균연봉이 500, 영업2팀은 200이 나왔습니다.
영업 1팀은 대표님 직속이라 대표님의 연봉도 포함되어 있습니다.
그러면 영업1팀의 직원들이 훨씬 많은 연봉을 받게 되는 걸까요?
이런 평균의 함정에 빠지는 걸 방지하기 위해 자료의 산포도(흩어짐 정도) 이용하게 됩니다.
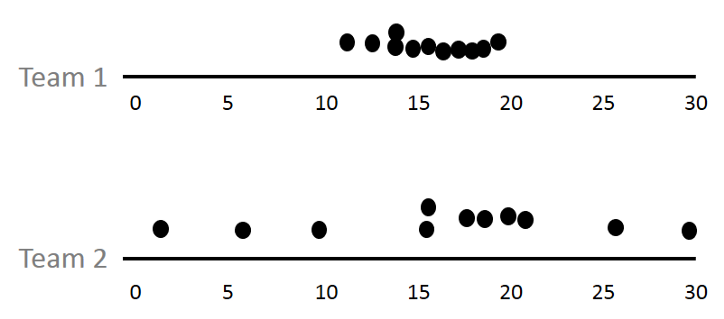
분산(표준편차)
각데이터와 평균의 차이를 각각 제곱한 합을 데이터 수로 나눈것으로, 데이터의 흩어짐 정도를 나타내는 값을 의미 합니다.
분산 = (표준편차)²
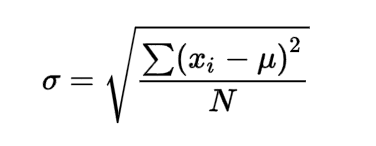
사분위수
사분위 범위 : 데이터 범위의 1/4, 3/4 까지의 폭 범위 : 데이터가 위치하는 폭, 최대값 - 최소값
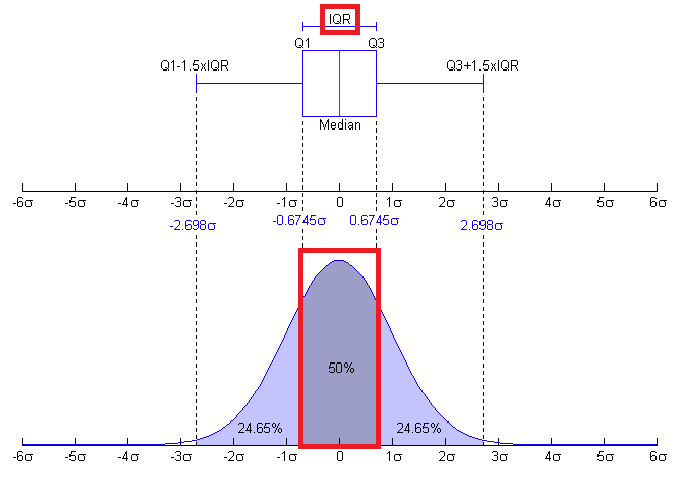
여기가지 대략적인 기초용어에대해서 알아 보았습니다.
다음에는 좀더 심화적인 내용을 알아보려고 합니다.
참고서적