대칭키와 공개키
데이터의 암호화에 있어서 가장 널리 사용되는 기법을 고르라면 반드시 대칭키와 공개키 암호화 기법이 꼽힌다. 이 중 대칭키는 우리의 일상에서도 흔히 보는 열쇠와 개념이 비슷하기 때문에 대칭키라는 기본 개념을 이해하는건 그리 어려운 일이 아니다. 그러나 공개키의 경우 일상에서 비슷한 개념을 접할 일이 없기 때문에 처음 공개키를 접할 때엔 알쏭달쏭하기 마련이다.
이번 포스트에서는 공개키 암호화 방식과 RSA에 대해서 아주 간단히 이야기 해보고자 한다.
공개키, 개인키
공개키에 대해 알아보기 시작하면 외부로 공개되는 공캐키니 소유자만 알아야 하는 개인키니 하는 이야기들이 시작된다.
암호화화 복호화를 문을 잠그고 여는 행위에 비유하자면, 대칭키는 하나의 열쇠로 문을 잠그고 여는 것이다.
공개키 기법은 열쇠가 2개다. 문을 잠글 수만 있는(=암호화) 열쇠가 있고, 문을 열 수만 있는(=복호화) 열쇠가 존재한다.
공개키 기법에서 암호화는 누구나 할 수 있어야 하기 때문에 암호화를 할 때 사용하는 키는 공개되어 있어야 한다. 그렇기 때문에 암호화를 하는 키는 공개키다.
암호화가 된 내용은 나만 복호화하여 볼 수 있어야 하며 절대로 키가 노출되어서는 안된다. 그래서 복호화를 하는 키는 개인키가 된다.
RSA
RSA는 큰 수를 소인수분해하기 힘들다는 점을 이용하여 등장한 공개키 알고리즘이다.
소인수분해 : 합성수를 소수들의 곱으로 나타내는 것.
합성수 : 여러 소수들의 곱셈으로 합쳐져서 이루어진 수.
공개키 알고리즘으로는 RSA, ECDSA, Rabin, Elgamal 등등이 있지만 사실 공개키 알고리즘을 사용한다고 하면 대부분이 RSA를 뜻할 정도로 RSA의 위상은 독보적이다. RSA보다 더 빠르고 더 좋은 보안수준을 제공하는 공개키 알고리즘도 있으나 RSA는 이미 표준이라는 점, 그리고 RSA의 근본적인 단점(양자컴퓨터 이슈)을 해결한 공개키 알고리즘이 마땅하지 않기에 당분간 RSA의 위상은 떨어지지 않을 것으로 보인다.
RSA 예시
보통 RSA 의 작동 예시를 들 때 p=17, q=11 값을 예시로 드는 경우가 많은데 여기서도 동일한 값으로 설명한다. 예시를 들기 전에 기본적으로 알아야할 사항은 아래와 같다.
공개키는 n, e 두 정수로 이루어진다.
개인키는 n, d 두 정수로 이루어진다.
Φ(n) 은 오일러 피 함수로 n 보다 작은 자연수들 중 n과 서로소인 자연수의 갯수이다.
-
공개키와 개인키를 만들기 위해 두 개의 소수 p, q를 선택한다. 여기서는 p=17, q=11 을 선택한다.
-
공개키와 개인키가 공유하는 값인 n 을 구한다. n은 p와q 곱셈으로 얻을 수 있다. 따라서 여기서 n은 17*11 = 187 이 된다.
-
Φ(n) 을 구한다. Φ(n)을 구하는 공식이 있지만, p와 q 둘 다 소수이므로 Φ(n) = (p-1) * (q-1) 형태로 퉁칠 수 있다. (소수는 자기자신보다 작은 모든 자연수와 서로소이기 때문) 식은 Φ(n) = (p-1) * (q-1) 으로, 16*10 = 160으로 Φ(n) 값은 160이 된다.
-
e를 구한다. e는 Φ(n)과 서로소인 수들 중에서 하나를 선택하면 된다. ( 1 < e < Φ(n) ) 여기서는 e = 7을 선택한다.
-
d를 구한다. (e * d) mod Φ(n) = 1 을 만족하는 d 값을 구한다. (1 + 160) / 7 = 23. d = 23
-
위 결과로 공개키 {187, 7}, 개인키 {187, 23} 을 얻었다.
-
이제 이 값들로 암호화와 복호화를 해보자. 암호화할 평문은 88이다.
- 암호화 = (평문 ^ e) mod n
- 88 ^ 7 mod 187 = 11
- 복호화 = (암호문 ^ d) mod n
- 32 ^ 23 mod 187 = 88
막 쓰기엔 너무나 비싼 RSA
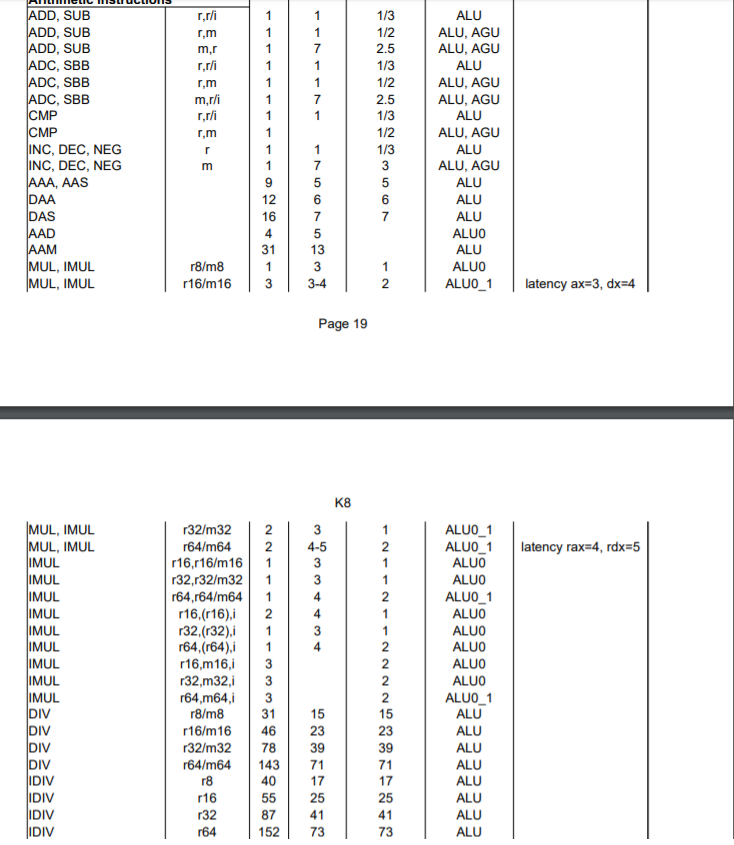
다뤄야 하는 숫자의 크기가 너무나 크다 보니 단순한 사칙연산을 수행하는데만도 무지막지한 CPU 파워가 소모된다. 게다가 주로 사용하게 되는 연산이 mod, 즉 나눗셈인데 기본적으로 나눗셈은 비싼 연산이며 수가 크면 클 수록 더욱 비싸진다.
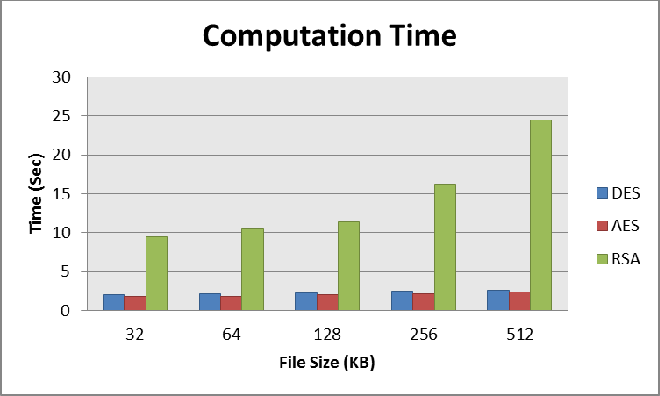
단순 수행 시간만 봐도 AES같은 대칭키에 비해 매우 시간이 오래걸리는걸 확인할 수 있다. 여기에 더해 키의 길이가 길어질 수록 RSA의 수행시간은 더욱 길어진다.
CPU의 발전으로 인해 예전보다는 RSA의 수행속도가 비약적으로 올라갔으나, 여전히 일반적인 통신에 적용하기엔 비용이 비싸다. 일반적으로 RSA는 암호화보다 복호화가 훨씬 비싼데 이런 특성 때문에 서버 사이드에서 사용하기에 더욱 부담스럽다.