들어가며
여러번 2D 게임을 만들기도 하고 즐기기도 하면서 여러가지 게임 그래픽에 대한 테크닉에 대해서 공부를 해보았습니다. 참고 - 울펜슈타인3D 는 과연 어떻게 3d를 구현했을까요?
이번에는 그 중에서 쿼터뷰에 대해서 이야기를 해보고자 합니다.

등축 투영법
먼저 기본되는 원리를 알려면 등축 투영법 을 알아야 합니다. 참조
원래는 제도 분야에서 많이 쓰이는 투영법 중 하나이지만, 게임 분야에서 복잡한 3D 계산을 하지 않고, 2D 그래픽만으로도 쉽게 표현할 수 있는 장점 때문에 많이 쓰이고 있습니다.

타일 기반 2D 게임
보통 2D 게임을 만들때 2D 좌표 기반으로 미리 그려진 이미지를 타일처럼 배치하는 형식으로 맵을 디자인하곤 합니다.


이번에 소개해드릴 쿼터뷰도 동일하게 타일처럼 맵을 디자인할 수 있습니다.

다만 쿼터뷰는 일반적인 2차원 좌표계랑 다른데 어떻게 구성해야 할까요?
Cartesian 좌표계 / Isometric 좌표계
일반적인 x/y 2차원 좌표계는 Cartesian 이라고 부릅니다.
일반적인 2d 타일맵을 아까 이야기 했던 등축 투영법 방식으로 표현한 것을 아까 이야기했던 쿼터뷰 혹은 isometric 이라고 부릅니다.
아래 사진처럼 수직축으로 45도 회전시킨 다음, 이어서 수평 축으로 +/- 35.264° [= arcsin(tan(30°))] 회전시킨 것과 같습니다.

그럼 어떻게 표현해야 할까요?
아래 이 이미지는 32x32 사이즈의 투명한 배경을 가진 이미지입니다.

쿼터뷰는 아래 사진을 이런식으로 배치하는 형식으로 시작됩니다.

단순히 이렇게 쌓는 것으로 끝입니다.
정리하자면 일반적인 2D 맵과 달리 isometric 은 아래와 같이 겹치는 구조로 되는 것 입니다.
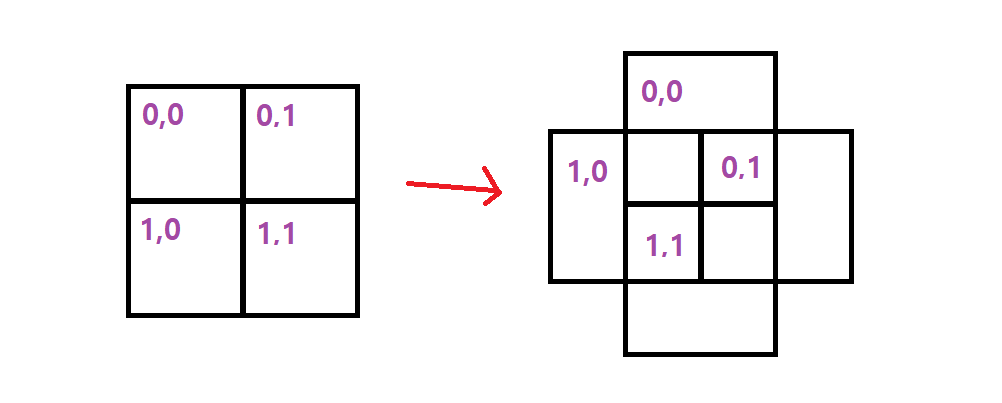
그렇다면 어떤 규칙으로 배치될까요?
식으로 표현하면
const isoX = cartX - cartY;
const isoY = (cartX + cartY) / 2;
isometric 의 x 좌표는 기존 좌표계에서 x - y 를 뺀 값이며 (게임내 구현은 첨부된 이미지의 너비만큼 곱해야 합니다.) y 좌표는 기존 좌표의 x + y 를 더한 값을 나눠야 합니다.
결과!
Ref.